데이터 수집하기
-데이터의 종류(내부 데이터, 직접 수집한 데이터, 외부 데이터)
-외부 데이터 얻는 사이트
1. 공공 데이터
-공공 데이터 포털(https://www.data.go.kr/)
-통계청 MDIS(https://mdis.kostat.go.kr/index.do)
-통계조사, 설문의 원자료(row data) 제공
-서울시 열린 데이터 광장(https://data.seoul.go.kr/)
2. 민간 데이터
-SKT 빅데이터 허브(bigdatahurb.co.kr)
-지역/시간대/업종별 통화량 데이터 등
-네이버 데이터랩(https://datalab.naver.com/)
-검색어 통계, 지역 업종 연령 성별 카드 사용 통계(BC카드)
-외국 사이트, 다양한 기업의 실제 데이터와 분석 사례
분석에 알맞게 데이터 가공하기
-분석의 종류
1. 확증적 데이터 분석
-정해진 목표에 따라
-미리 설정한 가설을 확인하기 위한 분석
-추정과 검정
-주로 연구에서 사용
2. 탐색적 데이터 분석
-분석 목표가 명확하지 않거나 데이터의 이해가 떨어질 때, 초기 분석 때 필수!
-변수 또는 변수간 관계 등 데이터 자체의 특성을 확인하기 위한 분석
-간단한 기술 통계량 계산, 다양한 그래프 활용
-모든 데이터 분석의 시작 단계에서 필수적인 과정
-요약과 모형
1. 요약
-데이터를 압축하는 과정
-데이터의 정보를 인식 가능한 수준으로 줄이는 과정
-그룹별로 관측치 수, 평균, 최댓값 계산 등 단순 숫자 요약
2. 모형(model)
-정해진 알고리즘에 따라 데이터 속 변수와 관측치 간 관계를 확인
-가능성을 수치화한 확률로 설명
-일종의 요약이지만 더 복잡
-데이터 가공의 필요성
>데이터 가공
-데이터 인식과 분석을 위해 데이터의 형태를 변환하는 과정
1. 부분 데이터 선택
-관심 있는(분석에 필요한) 관측치와 변수만 선택->나머지는 제거
2. 변수 결합, 분해 및 파생변수 생성
-기존 변수를 더 활용하기 좋은 형태로 변환
-ex) 나이(21세, 54세, ...) ->연령대(20대, 30대, ...)
적절한 방법으로 데이터 분석, 시각화, 문서화 하기
-분석 순서
1. 분석 목표 설정(실행 가능성, 활용 가능성 고려)
2. 데이터 수집(내부 및 관련 있는 외부 데이터 활용)
3. 탐색적 데이터 분석(변수나 변수간 관계에 대한 열린 분석 실행)
4. 확증적 데이터 분석/모형 적합(검정, 알고리즘 등을 활용해 분석)
-동일한 분석을 반복하여 결과의 재현 확인
-피드백을 통해 분석 목표 및 데이터 처리, 분석 방법 수정 고려
-이러한 과정을 거치면서 분석의 정교화 및 모형의 고도화
5. 분석 결과 공유
-분석 결과 시각화, 문서화 하기
1. 분석과 분석 결과 요약
-전체 과정이 아닌 흐름을 이해할 수 있는 수준으로 요약
-효과적인 정보 전달을 위한 그래프 활용 필요
>ms office(엑셀, 워드, 파워포인트 등) 활용 가능
>markdown(r, phython 등)에서 분석&보고서 작성
>대시보드:웹 기반으로 동적 보고서 작성 ex. R의 Shiny
데이터 분석의 재료인 데이터
1. 차이와 데이터
-데이터:변수(variable)와 관측치(observation)로 구성
-데이터 분석의 목적
>변수 속에서 관측치 간의 차이 확인
>변수 간의 관계를 확인
>차이와 관계를 확인하고 설명
-데이터 분석의 과정
>숫자와 그래프로 차이를 확인
>모형으로 차이를 설명
-차이
1. 절대적인 차이: 관측치의 실제 값이나 데이터를 요약
2. 상대적인 차이: 절대적인 차이를 상대적인 값으로 바꿈(ex. 시험 등수)
2. 범주형(categorical) 변수의 요약
-수준(levels)=처리=그룹
-요약하기
1. 수준별로 관측치 나누기
2. 수준별로 관측치 개수 세기
3. 표로 정리하기
-표와 차이
1. 빈도표(frequency table): 관측치 수를 정리, 수준간 절대적 차이
2. 상대빈도(relative frequency): 각 수준의 비율, 수준간 상대적 차이
-시각화
1. 막대 그래프: 빈도표 이용, 절대적인 차이
2. 원 그래프: 상대빈도 이용, 상대적인 차이
3. 순서대로 줄 세우는 수치형(numerical) 변수의 요약(정렬 이용)
-분위수(quantile):관측치들의 전반적인 분포를 확인
>사분위수(=다섯 숫자 요약): 최솟값, Q1(제 1 사분위수), 중앙값(제 2 사분위수), Q3(제 3 사분위수), 최댓값
-시각화
1. 상자그림(box plot): 사분위수로 나온 4개 구간의 길이 차이 확인, 3개 이상의 그룹 비교
2. 도수 분포표(frequency table): 구간화하여 표로 정리, 분포 확인
3. 히스토그램: 도수분포표를 높이로 표현, 각 구간의 비중 확인
4. 모두 더해 계산하는 수치형 변수의 또 다른 요약(합계 이용)
-평균(mean): 관측치들의 전반적으로 큰 정도
-분산/표준편차: 관측치들이 평균을 중심으로 흩어져 있는 정도
5. 수치형 변수를 상대적인 값으로 변환
-백분율(percentage): 특정 값 이하인 관측치의 수를 비율로 계산
-최소-최대 정규화(Min-Max normalization): (관측치-최소값)/(최대값-최소값), (결과의 범위: 0~1 사이)
-표준화(standardization): (관측치-평균)/표준편차
개념이 보이는 데이터 공간
1. 데이터와 공간의 개념
-데이터 공간: 데이터마다 다른 변수와 관측치 구성에 따라 만들어진 공간
>데이터의 차원: 변수의 수
>관측치 수만큼 점으로 표현
-데이터 공간과 분석의 재정의
1. 변수가 만들어내는 공간에서
2. 관측치들이 만들어 내는 차이를 숫자와 그래프로 확인
3. 더 자세히 상대적인 차이를 확인
4. 모형 등을 이용해 차이를 설명
-공간에서 범주형 변수 요약
>한 범주형 변수: 1차원에서 정해진 k개의 수준 중 하나의 값을 가짐
-공간에서 수치형 변수 요약
>한 수치형 변수: 1차원 수직선에서 다양한 값을 가짐
>평균: 1차원 공간의 무게중심
-1차원에서 2차원으로
1. 한 변수의 분석: 1차원에서 흩어진 패턴 파알, 주로 변수의 특성을 확인
2. 두 변수의 분석: 2차원에서 흩어진 패턴을 파악, 두 변수의 관계를 설명
2. 두 범주형 변수의 관계
-두 변수의 수준들 간의 관계로 확인
-교차표(분할표, contingency table): 2차원 표, 수준 조합에 대한 빈도표, 수준 조합의 절대적인 차이 확인
-열지도(heatmap): 2차원 교차표를 색으로 표현하여 시각화, 숫자 대신 색의 진하기로 표현
-행(열) 백분율: 행(열) 별로 상대빈도 계산, 각 수준의 전체 상대빈도와 비교, 상대적인 차이, 두 변수의 숨은 관계
3. 두 수치형 변수의 관계
1. 산점도(scatter plot) : 시각화
>2차원 공간에서 점의 패턴을 파악
>평균선의 교점=무게중심, 평균선 기준으로 4분면
>제 1, 3 사분면의 관측치 수가 높으면->두 변수가 양의 상관
제 2, 4 사분면의 관측치 수가 높으면->두 변수가 음의 상관
2. 공분산(covariance): 두 수치형 변수의 관계를 계산한 기술 통계량(절대적인 요약 값)
>공분산 공식:

>각 관측치가 중심(x_bar, y_bar)로부터 떨어진 면적/(n-1)
>큰 양수: 양의 상관
0에 가까울수록 관련 없음
큰 음수: 음의 상관
>단점: 단위 - scale(숫자가 큼), unit(단위가 다름)
3. 피어슨 상관계수(Pearson's correlation coefficient): 두 변수의 관계에 대한 상대적인 요약값
>두 변수를 표준화하여 공분산의 단위 문제를 해결, 표준화된 공분산
> 피어슨 상관계수 공식:
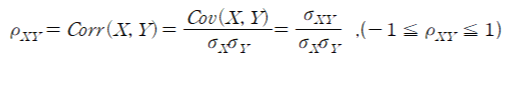
>rho_xy>0 :양의 상관
rho_xy=0 :상관x
rho_xy<0 :음의 상관
4. 한 범주형 변수와 한 수치형 변수의 관계
1. 범주형 변수를 그룹으로 활용해 수치형 변수의 그룹별 평균 계산
-조건부 평균(conditional mean)
>범주형 변수의 수준별로 수치형 변수의 평균 계산
>그룹(수준)에 따른 절대적인 차이 확인
>전체 평균과 비교하여 상대적인 차이 확인
-그룹별 상자그림 : 시각화
>각 수준별 상자그림을 동일한 축에 나란히 표현
>그룹간 분포 비교
2. 수치형 변수를 조건으로 활용해 범주형 변수의 조건부 비율 계산
-수치형 변수를 구간화:구간 값을 활용해 범주형 변수로 변환
-사실상 두 범주형 변수의 관계(교차표, 열지도 등 이용)
변수 유형 별 기술 통계량과 시각화 요약
| 첫번째 변수 | 두번째 변수 | 기술 통계량 | 시각화 |
| 범주형 | 범주형 | 교차표 | 열지도 |
| 수치형 | 수치형 | 상관계수 | 산점도 |
| 범주형 | 수치형 | 그룹별 평균 | 그룹별 상자그림 |
미래를 예측하는 회귀분석
1. 예측에 대한 개념
-관심변수(=반응변수=종속변수): 예측의 대상이 되는 변수
-설명변수(=독립변수)
-조건부 평균(conditional mean): 설명변수를 조건으로 계산한 종속변수의 평균
>범주형 설명변수 ->그룹별 평균
>수치형 설명변수 ->선형회귀
2. 산점도와 추세선
-수치형 설명변수를 이용한 예측
>수치형 설명변수의 구간화 ->그룹별 평균 계산
>산점도와 상관계수 활용
3. 선형 회귀 모형의 개념
-단순 선형 회귀(simple linear regression) 모형(model):

-회귀 모형 적합
>두 변수 X와 Y의 관계식을 확인하는 과정(beta_0, beta_1을 계산)
>결국 산점도에 가장 적절한 추세선을 찾는 것
4. 회귀 계수의 계산과 예측
-최소제곱법(Least Square Method)을 이용
>의미:예측값과 실제값 Y의 전반적인 차이가 적은 직선 찾기
>모든 회귀직선은 무게중심(x_bar, y_bar)을 지남
>회귀계수의 MLE(maximum likelihood estimation):

>회귀 직선의 기울기 beta_1은 두 변수의 상관계수에 비례
-회귀(regression)
>X가 꽤 커도 Y는 생각보다 작게 예측
>X가 꽤 작아도 Y는 생각보다 크게 예측
>예측된 Y값이 평균(중심)으로 당겨지는 효과
'데이터분석 > 이론' 카테고리의 다른 글
| [머신러닝]변수선택법, 교호작용 (0) | 2022.03.03 |
|---|---|
| [회귀분석, 머신러닝]회귀모델의 성능지표, 머신러닝 모델의 성능 지표 (0) | 2022.03.01 |
| [회귀분석]다중공산성 개념과 진단 방법 (0) | 2022.03.01 |
| [머신러닝 개념]모형의 적합성 평가 및 실험 설계 (0) | 2022.02.22 |
| [머신러닝 개념]머신러닝(Machine Learning)의 종류와 장단점, Tree 기반 모델 쓰는 이유 (0) | 2022.02.22 |