보스턴 주택 가격 데이터로 주택 가격을 예측하는 단순선형회귀분석을 한 뒤 결과를 해석해보겠습니다. 이 데이터는 1978년 데이터로 506개 타운의 주택 가격의 중앙값(단위 1,000 달러)이고, 예측변수(Y)는 Target(주택 가격)으로 연속형 변수이므로 회귀분석이 가능합니다. 나머지 13개의 설명변수(X)에 대한 설명은 다음과 같습니다.
CRIM: 범죄율
INDUS: 비소매상업지역 면적 비율
NOX: 일산화질소 농도
RM: 주택당 방 수
LSTAT: 인구 중 하위 계층 비율
B: 인구 중 흑인 비율
PTRATIO: 학생/교사 비율
ZN: 25,000 평방피트를 초과 거주지역 비율
CHAS: 찰스강의 경계에 위치한 경우 1, 아니면 0
AGE: 1940년 이전에 건축된 주택의 비율
RAD: 방사형 고속도로까지의 거리
DIS: 직업센터까지의 거리
TAX: 재산세율
분석에 들어가기 전, 필요한 라이브러리들을 불러옵니다. 회귀분석을 위해 필요한 라이브러리인 statmodels.api를 sm이라는 이름으로 불러옵니다.
> import pandas as pd
> import numpy as np
> import matplotlib.pyplot as plt
> import statmodels.api as sm
현재 경로의 아래에 있는 data 폴더에서 데이터를 불러온 뒤 head()함수를 이용하여 데이터를 확인합니다. 예측 변수인 Target과 13개의 설명변수들로 이루어져있습니다. drop() 함수를 이용하여 1개의 예측변수를 제외한 13개의 변수만 추출한 뒤 boston.data에 할당합니다.
> boston=pd.read_csv("./data/Boston_house.csv")
> boston.head()
AGE B RM CRIM DIS INDUS LSTAT NOX PTRATIO RAD ZN TAX CHAS Target
0 65.2 396.90 6.575 0.00632 4.0900 2.31 4.98 0.538 15.3 1 18.0 296 0 24.0
1 78.9 396.90 6.421 0.02731 4.9671 7.07 9.14 0.469 17.8 2 0.0 242 0 21.6
2 61.1 392.83 7.185 0.02729 4.9671 7.07 4.03 0.469 17.8 2 0.0 242 0 34.7
3 45.8 394.63 6.998 0.03237 6.0622 2.18 2.94 0.458 18.7 3 0.0 222 0 33.4
4 54.2 396.90 7.147 0.06905 6.0622 2.18 5.33 0.458 18.7 3 0.0 222 0 36.2
> boston.data=boston.drop(['Target'], axis=1) #설명변수만 추출
describe() 함수를 이용하여 추출한 설명변수들의 기술통계량(도수, 평균, 표준편차, 최소값, 제 1 사분위수, 중앙값, 제 3 사분위수, 최댓값)을 확인합니다.
> boston_data.describe()
AGE B RM CRIM DIS INDUS LSTAT NOX PTRATIO RAD ZN TAX CHAS
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean 68.574901 356.674032 6.284634 3.613524 3.795043 11.136779 12.653063 0.554695 18.455534 9.549407 11.363636 408.237154 0.069170
std 28.148861 91.294864 0.702617 8.601545 2.105710 6.860353 7.141062 0.115878 2.164946 8.707259 23.322453 168.537116 0.253994
min 2.900000 0.320000 3.561000 0.006320 1.129600 0.460000 1.730000 0.385000 12.600000 1.000000 0.000000 187.000000 0.000000
25% 45.025000 375.377500 5.885500 0.082045 2.100175 5.190000 6.950000 0.449000 17.400000 4.000000 0.000000 279.000000 0.000000
50% 77.500000 391.440000 6.208500 0.256510 3.207450 9.690000 11.360000 0.538000 19.050000 5.000000 0.000000 330.000000 0.000000
75% 94.075000 396.225000 6.623500 3.677082 5.188425 18.100000 16.955000 0.624000 20.200000 24.000000 12.500000 666.000000 0.000000
max 100.000000 396.900000 8.780000 88.976200 12.126500 27.740000 37.970000 0.871000 22.000000 24.000000 100.000000 711.000000 1.000000
단순 선형 회귀분석
단순 선형 회귀분석은 설명변수(X)와 예측변수(Y)가 각각 1개입니다. 여기서 예측변수를 Target으로 고정하고, CRIM(범죄율), AGE(1940년 이전에 건축된 주택의 비율), LSTAT(인구 중 하위 계층 비율)을 각각 설명변수로 하여 3번의 단순 선형 회귀분석을 하겠습니다.
Target~CRIM 적합
예측변수를 Target, 설명변수를 CRIM으로 하여 선형회귀분석을 진행하기 위해 먼저 CRIM 변수에 상수항을 추가하여 crim1 변수를 만듭니다.
> crim1=sm.add_constant(boston[['CRIM']], has_constant="add")
> crim1
const CRIM
0 1.0 0.00632
1 1.0 0.02731
2 1.0 0.02729
3 1.0 0.03237
4 1.0 0.06905
... ... ...
501 1.0 0.06263
502 1.0 0.04527
503 1.0 0.06076
504 1.0 0.10959
505 1.0 0.04741
sm.OLS() 함수를 이용하여 Target과 상수항을 추가한 crim1 변수로 선형 회귀모형을 적합시키고 fit()함수를 이용하여 fitted.model1에 저장한 뒤 summary() 함수로 결과를 출력합니다. R-squared(결정계수) 값이 0.151, adjusted R-squared 값이 0.149로 CRIM(범죄율) 변수가 예측변수를 잘 설명하지 못한다고 볼 수 있습니다. 상수항(coef)의 추정 계수(beta0_hat)는 24.0331이고 CRIM의 추정 계수(beta1_hat)는 -0.4152로 범죄율이 증가할수록 주택 가격이 감소한다고 볼 수 있고, 두 변수 모두 p값이 매우 작으므로 유의하다고 볼 수 있습니다.
> model1=sm.OLS(boston[['Target']], crim1)
> fitted_model1=model1.fit()
> fitted_model1.summary()
OLS Regression Results
Dep. Variable: Target R-squared: 0.151
Model: OLS Adj. R-squared: 0.149
Method: Least Squares F-statistic: 89.49
Date: Tue, 01 Mar 2022 Prob (F-statistic): 1.17e-19
Time: 14:39:11 Log-Likelihood: -1798.9
No. Observations: 506 AIC: 3602.
Df Residuals: 504 BIC: 3610.
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 24.0331 0.409 58.740 0.000 23.229 24.837
CRIM -0.4152 0.044 -9.460 0.000 -0.501 -0.329
Omnibus: 139.832 Durbin-Watson: 0.713
Prob(Omnibus): 0.000 Jarque-Bera (JB): 295.404
Skew: 1.490 Prob(JB): 7.14e-65
Kurtosis: 5.264 Cond. No. 10.1
위에서 계산한 추정 회귀계수(beta0, beta1)을 이용하여 예측변수의 추정값(y_hat)을 구합니다. 아래 식을 이용하여 np.dot() 함수로 직접 계산하거나 predict() 함수를 이용하여 계산할 수 있습니다.

> np.dot(crim1, fitted_model1.params)
> pred1=fitted_model1.predict(crim1) #결과 동일
분석한 결과를 이용해 시각화 해보겠습니다. x축을 CRIM, y축을 Target으로 하여 실제 데이터의 산점도와 적합한 선형 회귀 직선을 한 그래프에 그렸습니다.
> plt.scatter(boston[['CRIM']], boston[['Target']], label="data") #실제 데이터 산점도
> plt.plot(boston[['CRIM']],pred1,label="result", color="black") #적합한 회귀직선
> plt.legend()
> plt.show()
x축을 실제값(y), y축을 예측값(y_hat)으로 하여 산점도를 그린 결과 잘 맞지 않는 것으로 보입니다.
> plt.scatter(boston[['Target']],pred1)
> plt.xlabel("real_value")
> plt.ylabel("pred_value")
> plt.show()

resid.plot() 함수를 이용하여 y축을 잔차(residual)로 하여 잔차를 시각화한 결과, 예측이 잘 되었다고 보기 힘들고 CRIM(범죄율)을 이용하여 주택 가격을 예측하는 것이 어려워보입니다.
> fitted_model1.resid.plot()
> plt.xlabel("residual_number")
> plt.show()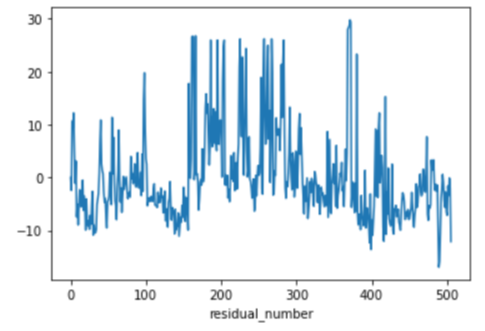
Target~AGE 적합
동일한 방법으로 예측변수를 Target, 설명변수를 AGE으로 하여 상수항을 추가하고 선형회귀분석을 진행합니다. 적합 결과, R-squared(결정계수) 값이 0.142, adjusted R-squared 값이 0.14로 CRIM과 마찬가지로 AGE(1940년 이전에 건축된 주택의 비율) 변수도 예측변수를 잘 설명하지 못한다고 볼 수 있습니다. 상수항(coef)의 추정 계수(beta0_hat)는 30.9787이고 AGE의 추정 계수(beta1_hat)는 -0.1232로 1940년 이전에 건축된 주택의 비율이 증가할수록 주택 가격이 감소한다고 볼 수 있고, 두 변수 모두 p값이 매우 작으므로 유의하다고 볼 수 있습니다.
> age1=sm.add_constant(boston[['AGE']], has_constant="add")
> model2=sm.OLS(boston[['Target']], age1)
> fitted_model2=model2.fit()
> fitted_model2.summary()
OLS Regression Results
Dep. Variable: Target R-squared: 0.142
Model: OLS Adj. R-squared: 0.140
Method: Least Squares F-statistic: 83.48
Date: Tue, 01 Mar 2022 Prob (F-statistic): 1.57e-18
Time: 15:17:59 Log-Likelihood: -1801.5
No. Observations: 506 AIC: 3607.
Df Residuals: 504 BIC: 3615.
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 30.9787 0.999 31.006 0.000 29.016 32.942
AGE -0.1232 0.013 -9.137 0.000 -0.150 -0.097
Omnibus: 170.034 Durbin-Watson: 0.613
Prob(Omnibus): 0.000 Jarque-Bera (JB): 456.983
Skew: 1.671 Prob(JB): 5.85e-100
Kurtosis: 6.240 Cond. No. 195.
위에서 계산한 추정 회귀계수(beta0, beta1)와 predict() 함수를 이용하여 예측변수의 추정값(y_hat)을 구합니다.
> pred2=fitted_model2.predict(age1)
분석한 결과를 이용해 시각화 해보겠습니다. x축을 AGE, y축을 Target으로 하여 실제 데이터의 산점도와 적합한 선형 회귀 직선을 한 그래프에 그렸습니다.
> plt.scatter(boston[['AGE']], boston[['Target']], label="data") #실제 데이터 산점도
> plt.plot(boston[['AGE']],pred2,label="result", color="black") #적합한 회귀직선
> plt.legend()
> plt.show()
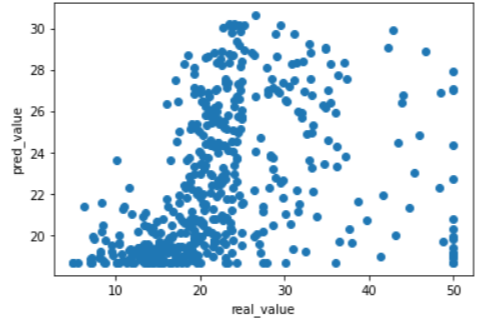
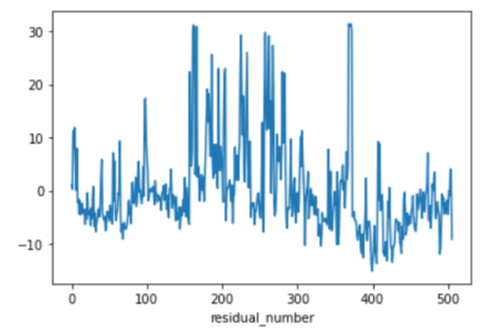
x축을 실제값(y), y축을 예측값(y_hat)으로 하여 산점도를 그린 결과 마찬가지로 잘 맞지 않는 것으로 보입니다. 잔차를 시각화한 결과 역시 예측이 잘 되었다고 보기 힘들고 AGE(1940년 이전에 건축된 주택의 비율)를 이용하여 주택 가격을 예측하는 것이 어려워보입니다.
> plt.scatter(boston[['Target']],pred2)
> plt.xlabel("real_value")
> plt.ylabel("pred_value")
> plt.show()
> fitted_model2.resid.plot()
> plt.xlabel("residual_number")
> plt.show()
Target~LSTAT 적합
마지막으로 예측변수를 Target, 설명변수를 LSTAT(인구 중 하위 계층 비율)으로 하여 상수항을 추가하고 선형회귀분석을 진행합니다. 적합 결과, R-squared(결정계수) 값이 0.544, adjusted R-squared 값이 0.543로 앞선 두 변수에 비해 예측변수를 잘 설명한다고 볼 수 있습니다. 상수항(coef)의 추정 계수(beta0_hat)는 34.5538이고 LSTAT의 추정 계수(beta1_hat)는 -0.95로 인구 중 하위 계층 비율이 증가할수록 주택 가격이 감소한다고 볼 수 있고, 두 변수 모두 p값이 매우 작으므로 유의하다고 볼 수 있습니다.
> lstat1=sm.add_constant(boston[['LSTAT']], has_constant="add")
> model3=sm.OLS(boston[['Target']], lstat1)
> fitted_model3=model3.fit()
> fitted_model3.summary()
OLS Regression Results
Dep. Variable: Target R-squared: 0.544
Model: OLS Adj. R-squared: 0.543
Method: Least Squares F-statistic: 601.6
Date: Tue, 01 Mar 2022 Prob (F-statistic): 5.08e-88
Time: 15:36:49 Log-Likelihood: -1641.5
No. Observations: 506 AIC: 3287.
Df Residuals: 504 BIC: 3295.
Df Model: 1
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 34.5538 0.563 61.415 0.000 33.448 35.659
LSTAT -0.9500 0.039 -24.528 0.000 -1.026 -0.874
Omnibus: 137.043 Durbin-Watson: 0.892
Prob(Omnibus): 0.000 Jarque-Bera (JB): 291.373
Skew: 1.453 Prob(JB): 5.36e-64
Kurtosis: 5.319 Cond. No. 29.7
위에서 계산한 추정 회귀계수(beta0, beta1)와 predict() 함수를 이용하여 예측변수의 추정값(y_hat)을 구합니다.
> pred3=fitted_model3.predict(lstat1)
분석한 결과를 이용해 시각화 해보겠습니다. x축을 AGE, y축을 Target으로 하여 실제 데이터의 산점도와 적합한 선형 회귀 직선을 한 그래프에 그렸습니다. 회귀직선이 data와 어느정도 잘 맞아보입니다.
> plt.scatter(boston[['LSTAT']], boston[['Target']], label="data") #실제 데이터 산점도
> plt.plot(boston[['LSTAT']],pred3,label="result", color="black") #적합한 회귀직선
> plt.legend()
> plt.show()
x축을 실제값(y), y축을 예측값(y_hat)으로 하여 산점도를 그린 결과 기울기가 1인 직선과 비슷하므로 어느정도 맞는 것으로 보입니다. 잔차를 시각화한 결과 역시 골고루 퍼져있으므로 예측이 잘 되었다고 볼 수 있습니다. CRIM, AGE, LSTAT 변수중 주택 가격 예측을 가장 잘 하는 변수는 LSTAT으로 보입니다.
> plt.scatter(boston[['Target']],pred3)
> plt.xlabel("real_value")
> plt.ylabel("pred_value")
> plt.show()
> fitted_model3.resid.plot()
> plt.xlabel("residual_number")
> plt.show()

'데이터분석 > Python' 카테고리의 다른 글
| [머신러닝]나이브 베이즈 모델(Naïve bayes clasification) in python (0) | 2022.03.10 |
|---|---|
| [범주형 자료분석]다중 로지스틱 회귀분석 예제- Personal Loan data - (1) in python (0) | 2022.03.08 |
| [기초]5가지 data type(list, tuple, set, dictionary, string) 총정리 in python (0) | 2021.08.29 |
