1. 필요한 개념
1. Decision boundary
2. 라그랑주 승수(Lagrange multiplier)
2. SVM(Support Vector Machine)
1. 정의
-decision rule
-cost function
-support vector
2. 특징
3. 차원의 저주
3. SVM(Support Vector Machine) 종류
1. SVM(Support Vector Classifier)
2. SVR(Support Vector Regression)
3. One-Class SVM
1. 필요한 개념
1. Decision boundary
-p차원에서 부등호를 사용하면 영역으로 나눌 수 있음
-x값이 decision boundary를 넘어감에 따라 Y의 예측값을 지정
-SVM뿐 아니라 다른 알고리즘에서도 사용
-decision boundary 식:
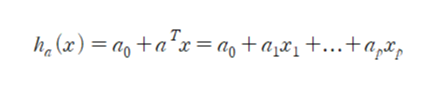
-a^T(a_1, a_2, ...)와 a_0에 따라 예측값이 바뀜, 이 값을 설정하는 과정이 머신러닝중 learning에 해당
-decision rule:
- h(x) > 0이면 식의 위쪽 영역
- h(x) < 0이면 식의 아래쪽 영역
2. 라그랑주 승수(Lagrange multiplier)
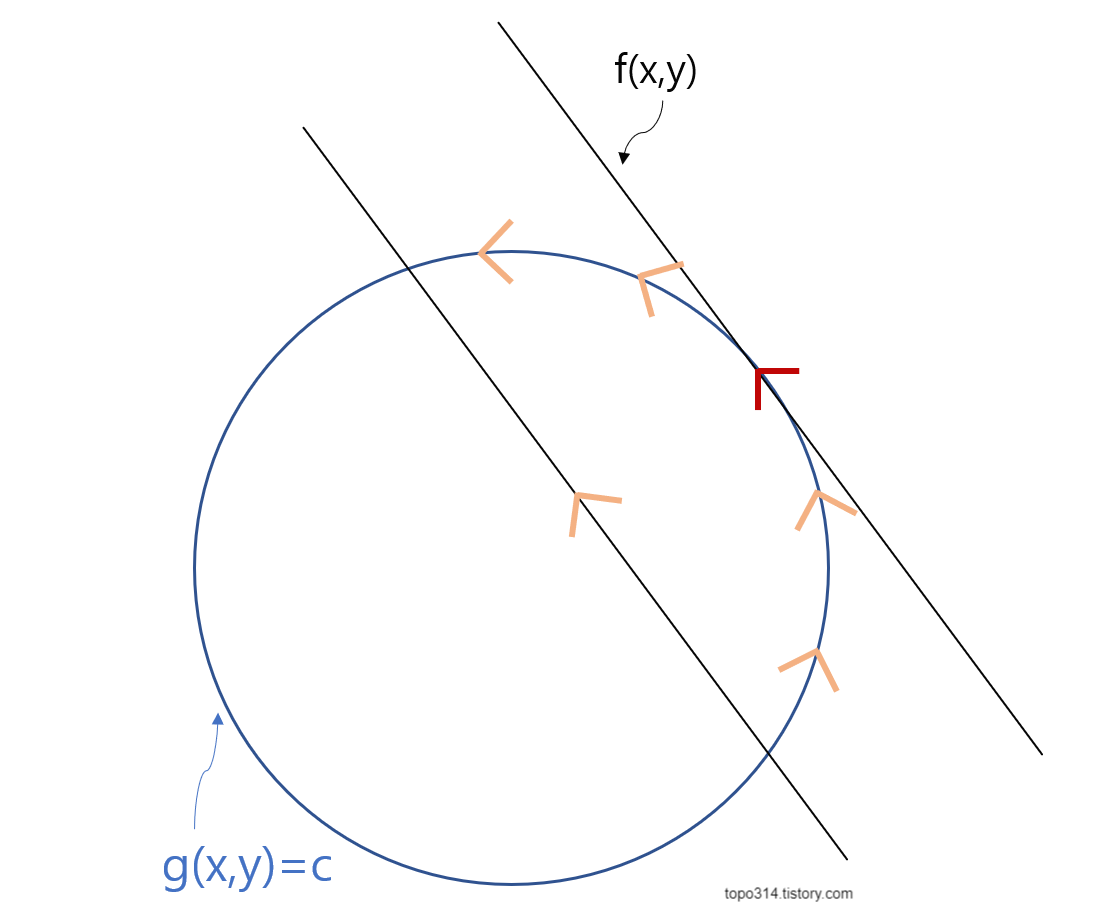
-최적화 문제(최소화or최대화 하는 값을 찾는 문제)를 풀 때, 목적함수( f(x,y) )를 최대화or최소화 하는 동시에 한정된 다른 조건( g(x,y)=c 등)을 주는 것
-f(x,y)와 제한식( g(x,y)=c )이 접할 때 f(x,y)가 극대값or극소값이 나옴
-f와 g의 변화량이 상수배(방향 동일)가 되는 지점
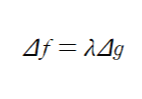
2. SVM(Support Vector Machine)
1. 정의
-데이터의 분포 가정이 힘들 때, 데이터를 잘 나누기 위해 margin을 최대화하는 boundary를 찾는 것
-정확히 구분되지 않으면 적당한 error를 허용하되 최소화하도록 boundary 결정
-초평면(hyper plane)을 아래 식으로 정의하고 beta, beta_0를 유일하게 만들기 위해 ||beta||=1로 제한
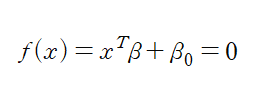
-decision rule: f(x)의 부호에 따라 Y의 부호 결정

-margin을 최대로 만드는 계수값 beta, beta0를 구하는 문제(xi: error, error의 합이 특정값을 넘지 않음)

-cost function 식: C(>=0)값이 클수록 error가 작음

-support vector: 정확히 margin의 경계 위에 있는 점(alpha_i가 0이 아닌 점), 이 값들로 초평면(beta)을 구함
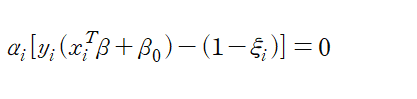
2. 특징
-보통 범주형 변수에 대해서
-model cost(ex. SSE)에 영향을 끼칠 점과 끼치지 않을 점을 margin을 통해 구분
-상대적 장점:
-데이터의 분포가정이 힘든 경우에도 boundary를 이용하여 사용 가능
-일반적으로 예측의 정확도 높음
-상대적 단점:
-C(in cost function)를 결정해야함
-모형 구축에 시간이 오래 걸림
3. 차원의 저주
-비선형 구조의 데이터를 적합할 때 커널(kernel)을 사용해야 함
=> degree polynomial이 일정 차원 이상이 되면 추정해야하는 모수의 개수가 많아져 test error가 높아짐(과적합)
3. SVM(Support Vector Machine) 종류
1. SVM(Support Vector Classifier)
-종속변수(Y)=범주형 변수인 경우
-margin안에 포함되거나 반대방향으로 분류된 점들(경계 부근)을 반영하여 model cost 계산
2. SVR(Support Vector Regression)
-종속변수(Y)=연속형 변수인 경우
-초평면, margine은 SVM과 동일하게 정의
-margin을 최대한 늘리면서 영역에 최대한 많은 점을 포함시키고, error(영역 바깥에 있는 점)를 최소화
=> margin 밖에 있는 점들의 error가 최소화되도록
-margin 바깥에 위치한 점들을 반영하여 model cost 계산
3. One-Class SVM
-종속변수(Y)의 정보가 없는 자료(하나의 class)를 요약(like unsupervised learning)
-자료를 모두 포함하는 원(boundary)을 활용
-중심 위치=a일때, R^2을 최소화하는 원의 반지름 R 찾기(error 허용)
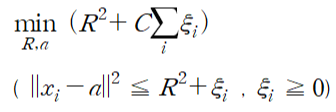
'데이터분석 > 이론' 카테고리의 다른 글
| [머신러닝]앙상블(Ensemble) 이론 (0) | 2022.03.13 |
|---|---|
| [머신러닝]의사결정나무(Decision Tree) 이론 (0) | 2022.03.13 |
| [머신러닝]k-Nearest Neighbors Algorithm(KNN) 이론 (0) | 2022.03.12 |
| [머신러닝]나이브 베이즈(Naïve bayes classifier) 이론 (0) | 2022.03.10 |
| [머신러닝]회귀계수 축소법 (0) | 2022.03.08 |



