1. k-Nearest Neighbors Algorithm(KNN)
1. 정의
2. 특징
3. 거리 구하는 법
4. k 결정
5. 차원의 저주
2. Cross-validation
k-fold cross validation:
3. k-Nearest Neighbors Algorithm 종류
1. 종속변수(Y)=범주형 변수인 경우
2. 종속변수(Y)=연속형 변수인 경우
1. k-Nearest Neighbors Algorithm(KNN)
1. 정의
-주변 sample k개의 정보를 이용하여 새로운 관측치의 종속변수(Y)를 예측
-N개의 관측치(x,y)에 대하여 거리 순으로 정렬
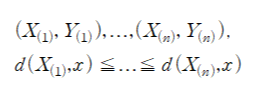
-종속변수(Y)=범주형 변수일때: m번째 범주일 확률(: m번째 범주 개수/k)이 가장 큰 그룹이 y의 추정값

-종속변수(Y)=연속형 변수일때: 근처 k개의 평균을 선택(inverse distance weighted average를 고려할 경우 아래 식 사용)

2. 특징
-k에 따라 성능 달라짐
-majority voting이므로 거리에 반비례하는 weight를 줄 필요가 있음(가까울수록 가중치↑)
-중요한 변수와 불필요한 변수가 섞여있다면 중요한 변수를 선별해야 효율이 높음
3. 거리 구하는 법
-범주형 변수일때:
-해밍 거리(hamming distance): 같으면 거리가 0, 다르면 1
-수식:

-연속형 변수일때:
-유클리드 거리(Euclidian distance): 대각선으로 가로지르는 거리
-수식:

-맨해튼 거리(Manhattan distance): 택시거리, x축&y축과 평행하게 가는 거리
-수식:
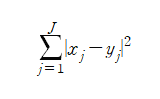
4. k 결정
-k가 너무 크면 미세한 경계부분을 잘못 분류
-k가 너무 작으면 과적합 우려, 이상치의 영향을 크게 받음, 패턴이 직관적이지 않음
-test error가 최소인 k로 결정(일반적으로 test error는 감소하다가 증가하는 추세)
-cross-validataion 이용
5. 차원의 저주
-차원이 증가함에 따라 전체 영역에 비해 설명할 수 있는 영역이 점점 줄어듦
=> KNN에서 극대화됨
-차원 축소(PCA: Principal Compenent Analysis 등) 또는 feature selection(: 유의한 변수만 추려냄) 후에 KNN 적합
2. Cross-validation
-과적합, smaple loss를 동시에 해결하기 위해 사용
-traing set을 가장 잘 맞히는 머신은 test set에서는 잘 동작하지 않을 수 있음(모델이 복잡할수록)
-training error는 error를 과소추정하므로 test error가 높아질 수 있음
=> test error를 구하려면 데이터를 나눠야 하므로 데이터의 소실(sample loss)이 발생
-error를 과소추정하지 않으면서 데이터의 소실을 최소화하기 위해 데이터를 번갈아가며 training, test로 나눔
-k-fold cross validation:
-장점: error를 전체 데이터에서 다 구할 수 있음, 전체 데이터로 모델 적합
1. 전체 데이터를 training data와 test data로 나눔
2. training data를 k개의 fold로 나눈 후 n번째 split에서 fold n(n번째 데이터)을 test, 나머지를 training으로 사용(n=1, 2, ..., k)
3. 여기서 나머지인 training data로 모델 구하고 fold n인 test data로 error 추정
4. k 추정

3. k-Nearest Neighbors Algorithm 종류
1. 종속변수(Y)=범주형 변수인 경우
-k-nearest neighbors중 가장 많이 나타나는 범주로 y를 추정
-tie(동점) 문제를 막기 위해 k는 홀수로 정하는 것이 좋음
2. 종속변수(Y)=연속형 변수인 경우
-k-nearest neighbors의 대표값(평균)으로 y를 추정
-Inverse distance weighted average(거리에 반비례하는 가중치) 고려 가능
'데이터분석 > 이론' 카테고리의 다른 글
| [머신러닝]의사결정나무(Decision Tree) 이론 (0) | 2022.03.13 |
|---|---|
| [머신러닝] SVM(Support Vector Machine) 이론 (0) | 2022.03.12 |
| [머신러닝]나이브 베이즈(Naïve bayes classifier) 이론 (0) | 2022.03.10 |
| [머신러닝]회귀계수 축소법 (0) | 2022.03.08 |
| [범주형 자료분석]로지스틱회귀분석(Logistic regression) (0) | 2022.03.08 |



