1. 나이브 베이즈 모델(Naïve bayes classifier)
1. 정의
2. 특징
2. 나이브 베이즈 모델(Naïve bayes classifier) 종류
1. Gaussian Naïve bayes classifier(가우시안 나이브 베이즈)
2. Multinomial Naïve bayes classifier(다항 나이브 베이즈, 멀티노미얼 나이브 베이즈)
3. Bernoulli Naïve bayes classifier(베르누이 나이브 베이즈)
1. 나이브 베이즈 모델(Naïve bayes classifier)
1. 정의
-'어떤 속성이 주어졌을 때 반응변수가 c일 확률'은 '어떤 속성이 주어지고 반응변수가 c일 확률(교집합)'과 비례
-다시말해, 이는 '반응변수가 c일때 어떤 속성일 확률'과 '반응변수가 c일 확률'의 곱과 비례
-수식:

-조건부 독립, 베이즈 정리 사용
-반응변수가 Yes, No로 이항이라면 둘 중 확률이 더 큰 것을 선택하기 위해 (위 수식의) 분자를 비교
-마지막줄 식을 가장 크게 만드는 c를 Y로 예측
2. 특징
-속성=입력변수=독립변수
-반응변수는 따로 떼어서 생각
-나이브 베이즈의 특징: 설명변수간의 상호독립을 가정
=> 계산 간단, 샘플수가 많지 않아도 계산&모델링 가능
-모델을 간단하게 만드는데도 불구하고 예측정도가 상당히 준수함(오분류율이 높지 않음)
2. 나이브 베이즈 모델(Naïve bayes classifier) 종류
1. Gaussian Naïve bayes classifier(가우시안 나이브 베이즈)
-설명변수(X)가 연속형인 경우
-X를 정규분포로 가정
- y = 1, ... ,C
- P( X=x | y=c )가 정규분포를 따름(표본 평균, 표본 분산)

-수식:
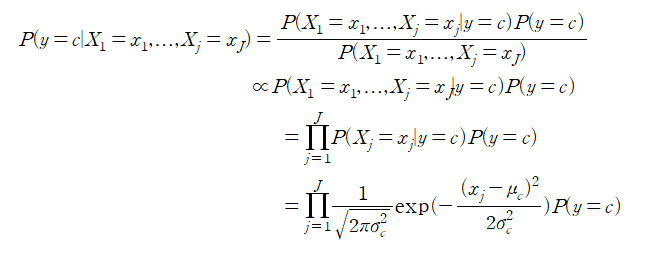
2. Multinomial Naïve bayes classifier(다항 나이브 베이즈, 멀티노미얼 나이브 베이즈)
-설명변수(X)가 범주형인 경우
-X를 다항분포로 가정
- y = 1, ... ,C , k = 1, ... ,k
- y가 c일때 X가 특정 범주일 확률은 다항분포를 따름

-수식:

3. Bernoulli Naïve bayes classifier(베르누이 나이브 베이즈)
-설명변수(X)가 이분형인 경우(다항 나이브 베이즈가 더 일반적)
-X를 이항분포로 가정
- x = 0, 1
- P( X=x | y=c )는 이항분포를 따름

'데이터분석 > 이론' 카테고리의 다른 글
| [머신러닝] SVM(Support Vector Machine) 이론 (0) | 2022.03.12 |
|---|---|
| [머신러닝]k-Nearest Neighbors Algorithm(KNN) 이론 (0) | 2022.03.12 |
| [머신러닝]회귀계수 축소법 (0) | 2022.03.08 |
| [범주형 자료분석]로지스틱회귀분석(Logistic regression) (0) | 2022.03.08 |
| [머신러닝]회귀분석 진단, 다항회귀분석 (0) | 2022.03.06 |



