회귀계수 축소법
1. 회귀계수 축소법 - Ridge 회귀
2. 회귀계수 축소법 - Lasso 회귀
3. Ridge 회귀와 Lasso 회귀의 차이점
4. 회귀계수 축소법 - Elastic-Net 회귀
회귀계수 축소법
-출력변수(Y)에 영향력이 적은 입력변수(X)의 계수를 0에 가깝게 만들어 제거하는 식으로 중요한 변수만 남기는 방법
-장점:
1) 잡음(noise)을 제거해 모형의 정확도를 개선(예측력이 올라감)
2) 모형의 연산 속도가 빨라짐
3) 다중공산성 문제를 조금이나마 완화킬 수도 있음 => 모형의 해석 능력을 향상
-종류: Ridge 회귀, Lasso 회귀, Elastic-Net 회귀
-SSE와 f(beta)의 합을 최소화 시키도록
-일반적으로 다중공산성이 있다면 Ridge, Elastic-Net 회귀의 예측 성능이 좋음, 목적에 맞게 사용!
1. 회귀계수 축소법 - Ridge 회귀
-f(beta): 회귀계수의 제곱의 합
-람다(lambda): tuning parameter, 클수록 많은 회귀계수(beta)가 0으로 수렴(완전히 0이 되진 않음)
=> 아주 적은 값이라도 예측에 많은 beta를 사용하므로 Y 예측에 도움

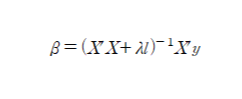
-다중공산성은 X들간의 강한 선형관계로 인해 (X'X)의 역행렬을 구할 수 없으므로 이 값에 lambda를 추가하여 역행렬 계산이 가능함
-예측 성능을 최대한 높이고 싶을 때 사용
2. 회귀계수 축소법 - Lasso 회귀
-f(beta): 회귀계수의 절대값의 합
-람다 값이 증가할수록 회귀계수의 값이 0으로 수렴(완전히 0으로 감)
=> 회귀계수가 0이 되므로 회귀계수 선택(추출) 가능
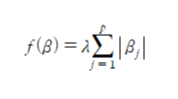
-중요한 변수여도 제거될 수 있으므로, 성능보단 몇개의 변수만 남기고 싶을 때 사용
-validation의 성능이 높아야 좋으므로 validation data로 람다 값을 변화시키며 MSE가 최소일 때의 람다를 탐색
3. Ridge 회귀와 Lasso 회귀의 차이점
-둘 다 lambda 값이 커질수록 회귀계수가 0에 가까워지지만, Ridge는 0이 되지 않고 Lasso는 완전히 0으로 축소함
-Ridge 회귀:
1) 입력변수(X)들이 전반적으로 비슷한 수준으로 출력 변수에 영향을 미치는 경우 사용
2) 한번에 구할 수 있음
-Lasso 회귀:
1) 출력변수(Y)에 미치는 입력변수의 영향력 편차가 큰 경우 사용
2) 최적화 기법을 통해 구해야함
3) 회귀계수를 0으로 만들어서 특정 변수만 뽑을 수 있음
4. 회귀계수 축소법 - Elastic-Net 회귀
-Lasso와 Ridge를 결합한 하이브리드(정규화) 회귀 모델
-f(beta): Lasso의 회귀계수 절대값 + Ridge의 회귀계수 제곱합
-람다를 통해 두 방법의 강도 조절

-Lasso와 Ridge의 장점을 결합
-grouping effect(상관성이 있는 여러 변수들의 correlation이 커질 때 한번에 제거/선택) 유도
-예측 성능을 최대한 높이고 싶을 때 사용
'데이터분석 > 이론' 카테고리의 다른 글
| [머신러닝]k-Nearest Neighbors Algorithm(KNN) 이론 (0) | 2022.03.12 |
|---|---|
| [머신러닝]나이브 베이즈(Naïve bayes classifier) 이론 (0) | 2022.03.10 |
| [범주형 자료분석]로지스틱회귀분석(Logistic regression) (0) | 2022.03.08 |
| [머신러닝]회귀분석 진단, 다항회귀분석 (0) | 2022.03.06 |
| [머신러닝]변수선택법, 교호작용 (0) | 2022.03.03 |


